LE BINAIRE

A) Le codage binaire

        Vers la fin des années 30, Claude Shannon* [1916-2001] utilise une formule à la fois simple et ingénieuse pour permettre de coder les informations dans les disque durs. Ce codage de l’ information est appelé base binaire (base 2) qui consiste à utiliser deux états ( représentés par les chiffres 0 et 1).
Le terme bit signifie <<binary digit>>, 0 ou 1 en numérotation binaire. Il s’agit de la plus petite unité d’information manipulable par une machine. Cette information est peut être représenté physiquement par un signal magnétique ou électrique qui correspond à 1 au delà d’un certain seuil. Avec un bit, il est possible d’obtenir deux états soit 1 soit 0. Pour un groupe de n bits, il est possible de représenter 2 n valeurs.

Valeur de 3 bits	Valeur décimal
000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

 

       Dans un nombre binaire, la valeur d’un bit, appelé poids, dépend de la position du bit en partant de la droite. A la manière des dizaines, centaines et des milliers, pour un nombre décimal, le poids d’un bit croît d’une puissance de deux en allant de la droite vers le gauche.
Par exemple, le nombre 1001 en binaire :  23*1+22*0+21*0+20*1= 9 ainsi on passe d’une information binaire à une valeur décimale.

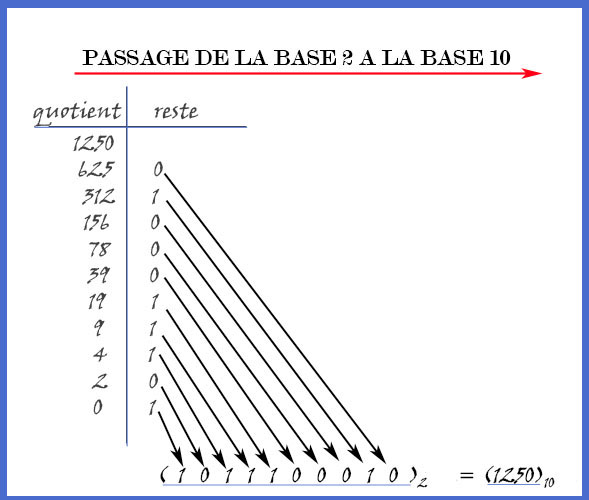
       En fonction de la difficulté, c'est à dire de la grandeur du nombre binaire, on peut ou pas utiliser la divison par 2, comme ci-dessous :